Smoothing with DemoTools

Jose Manuel Aburto, Ilya Kashnitsky, Marius Pascariu, Tim Riffe

2022-01-17

Source: vignettes/smoothing_with_demotools.Rmd

How to use DemoTools to smooth population counts

Smoothing data over age is traditionally intended to have plausible/corrected estimates of population counts from census data. Smoothing procedures help to derive figures that are corrected primarily for net error by fitting different curves to the original 5 or 10-year totals, modifying the original counts (Siegel Jacob and Swanson David 2004). Several methods have been developed for this aim and the major smoothing methods are included in DemoTools. Including the Carrier-Farrag (Carrier and Farrag 1959), Arriaga (Arriaga, Johnson, and Jamison 1994), Karup-King-Newton, United Stations (United Nations 1955), Spencer (Spencer 1987) and Zelnik methods. Below we briefly give an overview of the method and apply them to the male Indian population in 1991.

library(DemoTools)
#> Loading required package: Rcpp

# 'pop1m_ind' available as package data
Value <- pop1m_ind
Age   <- 0:(length(Value)-1)

plot(Age, Value/sum(Value), type = 'l',
     ylab = 'Proportion of population',
     xlab = 'Single age',
     main = 'Unsmoothed population')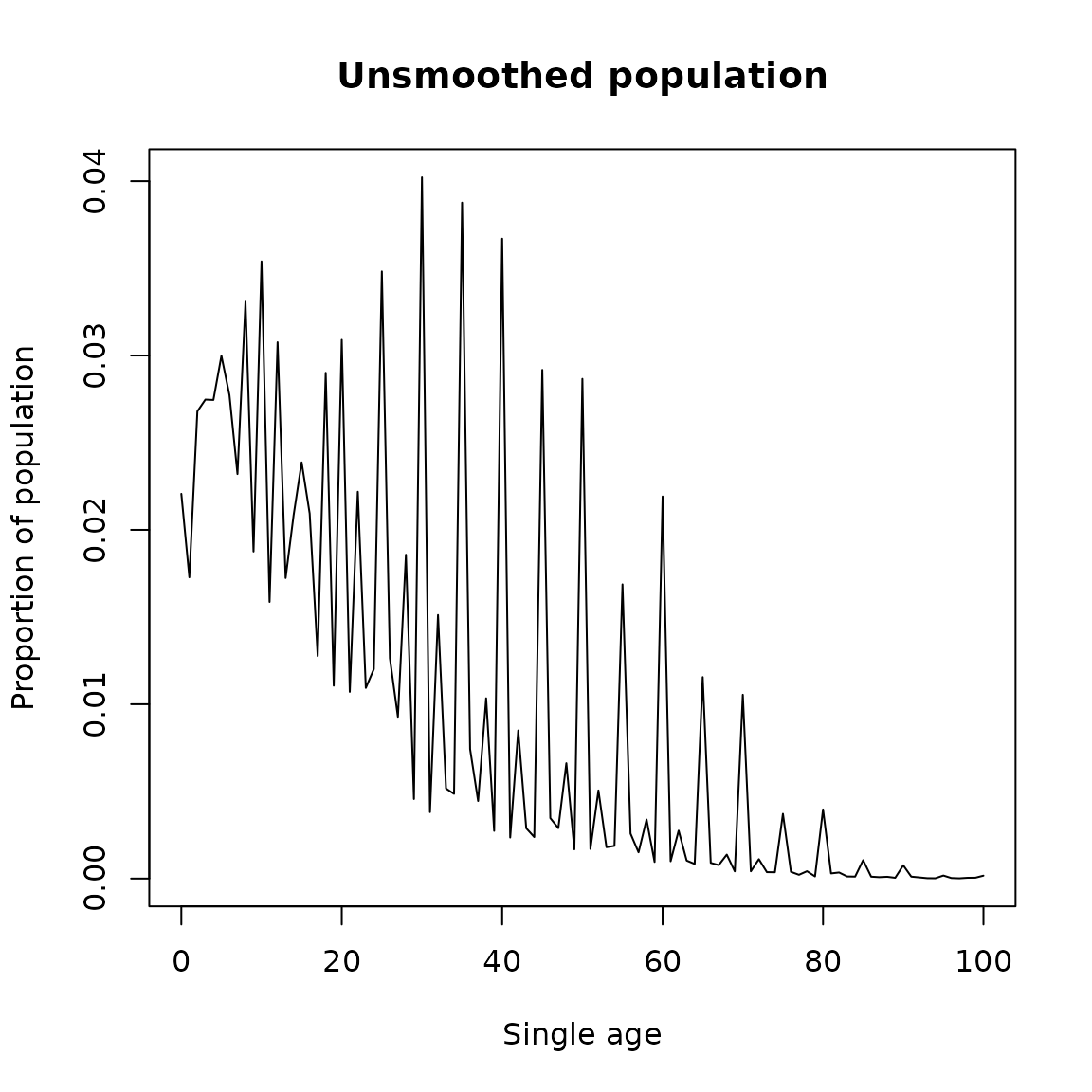

Carrier-Farrag

This method considers the ratio, \(K\), of the population in one five-year age-group to the next one (Carrier and Farrag 1959). If \(v_0\) is a ten-year age-group, and \(v_{-2}\) and \(v_2\) are the preceding and succeeding age-groups, respectively, and if \(K^4 = v_{-2}/v_2\). Then, the older five-year group \(v_1\) can be estimated by \(v_0/(1+K)\). This equation connects the population in two ten-year age groups separated by an interval of ten years. Therefore the value \(K\) can be seen as the middle point between the two ten-year age groups. To run this method in DemoTools the function afesmth is used with the option ‘Carrier-Farrag.’ The figure below shows the smoothed population by five-year age groups.


cf <- smooth_age_5(
  Value = Value,
  Age = Age,
  method = "Carrier-Farrag",
  OAG = TRUE
)

plot(seq(0,100,5),cf/sum(cf), type= 'l',
     ylab = 'Proportion of population',
     xlab = 'Age-group',main = 'Smoothed population with Carrier-Farrag',xaxt='n')
axis(1, labels = paste0(seq(0,100,5),'-',seq(4,104,5)), at =seq(0,100,5))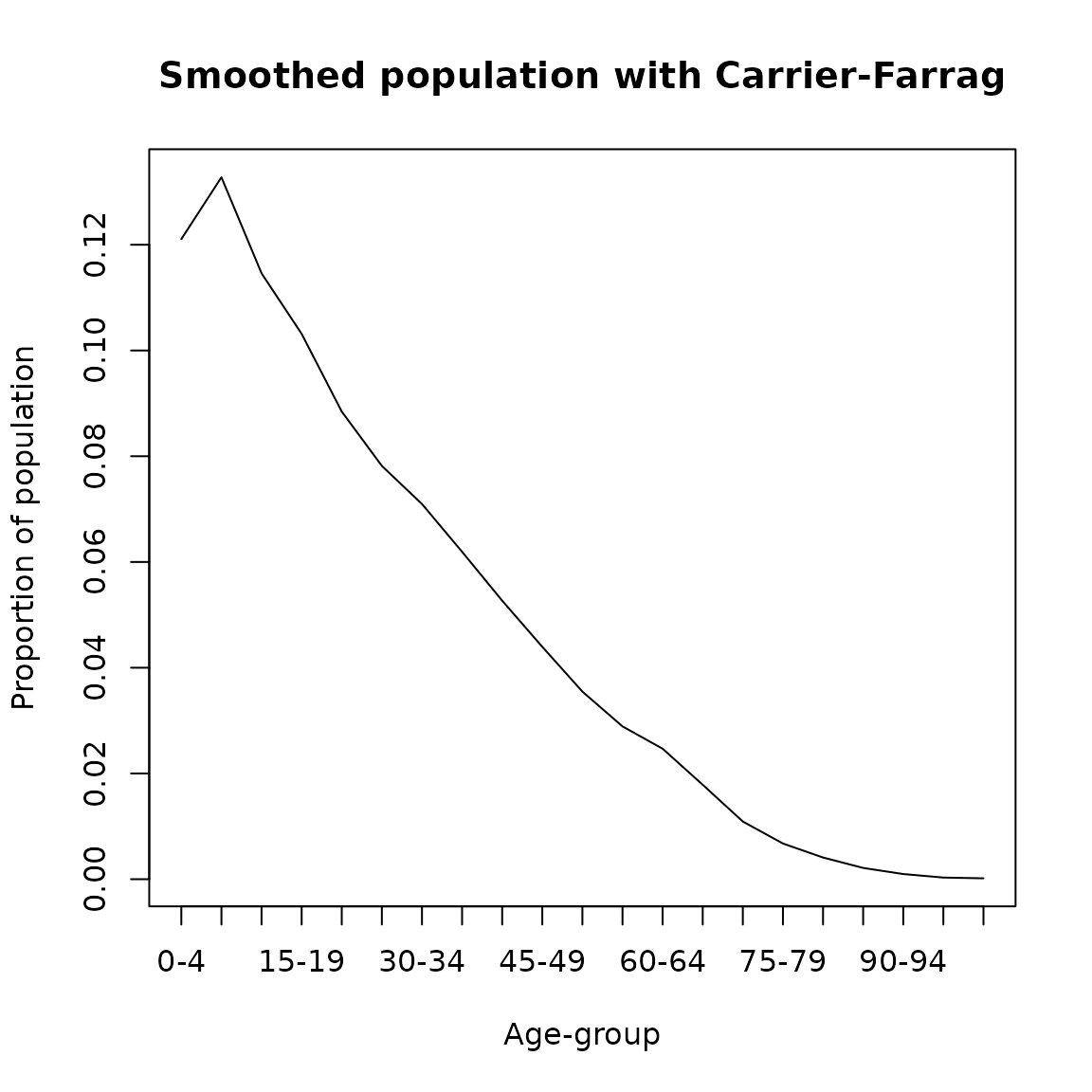

Arriaga

Similarly to the previous method, when the 10-year age group to be separates is the central group of three, the following formulas are used in this method (Arriaga and others 1968):

\[\begin{equation*} _{5}P_{x+5} = \frac{-_{10}P_{x-10}+11 _{10}P_{x+10}+2 _{10}P_{x+10}}{24} \end{equation*}\] and \[\begin{equation*} _{5}P_{x} = _{10}P_{x} - _{5}P_{x+5} \end{equation*}\]

Where: \(_{5}P_{x+5}\) is the population between ages \(x+5\) and \(x+9\); \(_{10}P_{x}\) is the population between ages \(x\) and \(x+9\); and \(_{5}P_{x}\) is the population between ages \(x+\) and \(x+4\). When the 10-year age group to be separated is an extreme age group (the youngest or the oldest), the formulas are different. For the youngest age group, the following formulas are used:

\[\begin{equation*} _{5}P_{x+5} = \frac{8 _{10}P_{x}+ 5 _{10}P_{x+10} - _{10}P_{x+20}}{24} \end{equation*}\] and \[\begin{equation*} _{5}P_{x} = _{10}P_{x} - _{5}P_{x+5} \end{equation*}\]

and for the last age group the coefficients are reversed:

\[\begin{equation*} _{5}P_{x} = \frac{ -_{10}P_{x-20}+ 5 _{10}P_{x-10}+ 8 _{10}P_{x}}{24}. \end{equation*}\]

To perform this model the option ‘Arriaga’ must be chosen in the ‘agesmth’ function.


cf <- smooth_age_5(
  Value = Value,
  Age = Age,
  method = "Arriaga",
  OAG = TRUE
)

plot(seq(0,100,5),cf/sum(cf), type= 'l',
     ylab = 'Proportion of population',
     xlab = 'Age-group',main = 'Smoothed population with Arriaga',xaxt='n')
axis(1, labels = paste0(seq(0,100,5),'-',seq(4,104,5)), at =seq(0,100,5))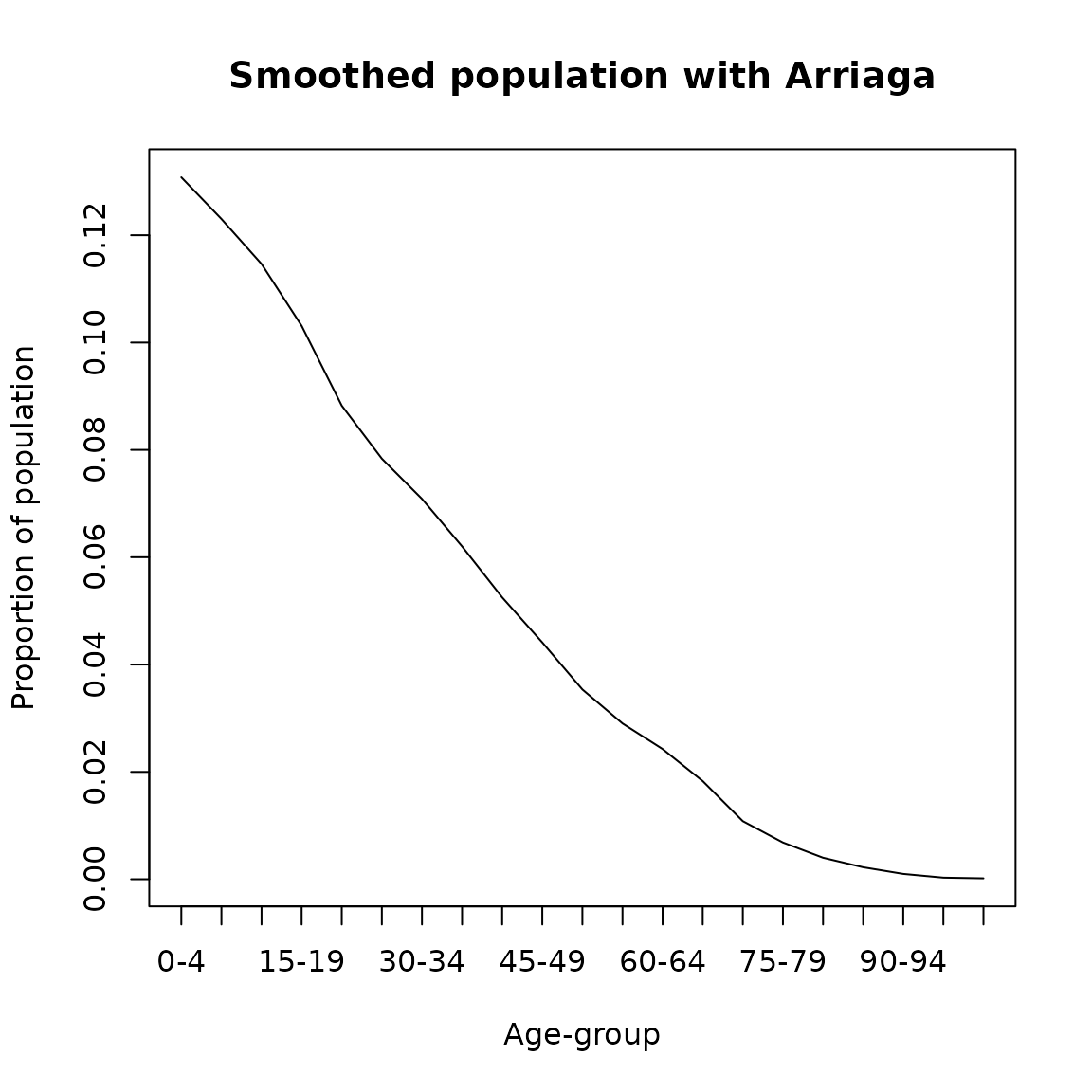

Karup-King-Newton

Following the same logic, the KKN method uses the following formulas:

\[\begin{equation*} _{5}P_{x} = \frac{1}{2} _{10}P_{x} + \frac{1}{16} \big( _{10}P_{x-10} - _{10}P_{x+10} \big) \end{equation*}\] and \[\begin{equation*} _{5}P_{x+5} = _{10}P_{x} - _{5}P_{x}. \end{equation*}\]

To implement this smoothing process select the KKN in the agesmth function.

# TODO smooth_age_5 is throwing an internal error
# Error in tapply(Value, AgeN, sum) : arguments must have same length

cf <- smooth_age_5(
  Value = Value,
  Age = Age,
  method = "KKN",
  OAG = TRUE
)

plot(seq(0,100,5),cf/sum(cf), type= 'l',
     ylab = 'Proportion of population',
     xlab = 'Age-group',main = 'Smoothed population with Karup-King-Newton ',
     xaxt='n')

axis(1, labels = paste0(seq(0,100,5),'-',seq(4,104,5)), at =seq(0,100,5))

United Nations

The United Nations (Carrier and Farrag 1959) developed the following formula to smooth population counts \[\begin{equation} _5\hat{P}_x = \frac{- _5P_{x-10} + 4\, _5P_{x-5} + 10\, _5P_{x} +4\, _5P_{x+5} - _5P_{x+10}}{16} \end{equation}\]

where \(_5\hat{P}_x\) represents the smoothed population between ages \(x\) and \(x+4\). This method can be applied in DemoTools using the "United Nations method of smooth_age_5() as follows


un_result <- smooth_age_5(Value = Value,Age = Age,method="United Nations",OAG = T)
plot(seq(0,100,5),un_result/sum(un_result,na.rm = T), type= 'l',
    ylab = 'Proportion of population',
     xlab = 'Age-group',main = 'Smoothed population with UN Method',xaxt='n')
axis(1, labels = paste0(seq(0,100,5),'-',seq(4,104,5)), at =seq(0,100,5))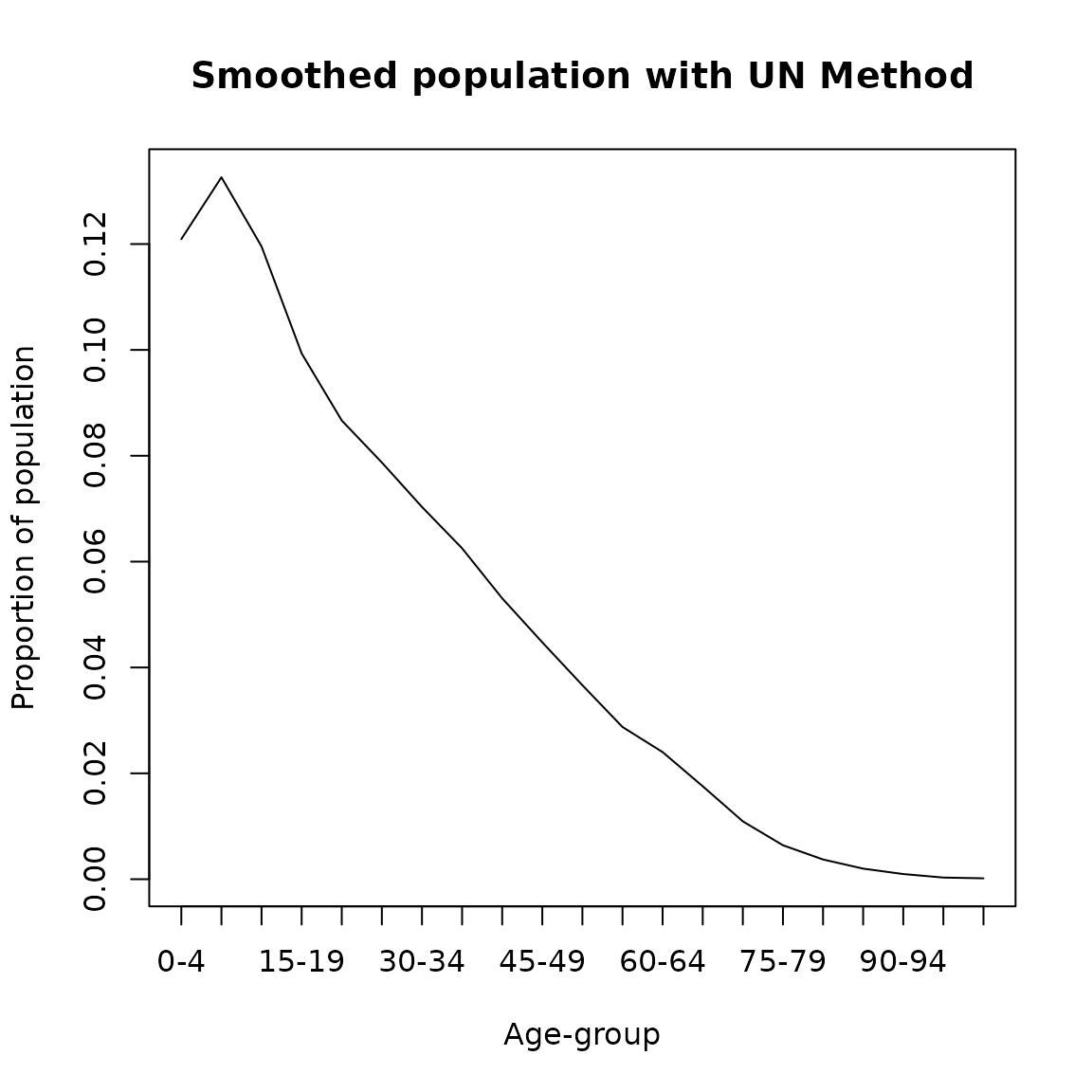

Strong

The Strong formula adjusts proportionally the smoothed 10-year age groups to the census population in those ages, after this procedure the 10-year age groups can be subdivided into 5-year age groups (Arriaga and others 1968)

\[\begin{equation} _{10}\hat{P}_x = \frac{_{10}P_{x-10} + 2\, _10P_{x} + _{10}P_{x+10}}{4} \end{equation}\]

where \(_{10}\hat{P}_x\) represents the smoothed population ages \(x\) to \(x+9\). It is implemented in DemoTools as follows


strong_result <- smooth_age_5(Value = Value,Age = Age,method="Strong",OAG = T)
plot(seq(0,100,5),strong_result/sum(strong_result,na.rm = T), type= 'l',
    ylab = 'Proportion of population',
     xlab = 'Age-group',main = 'Smoothed population with Strong formula',xaxt='n')
axis(1, labels = paste0(seq(0,100,5),'-',seq(4,104,5)), at =seq(0,100,5))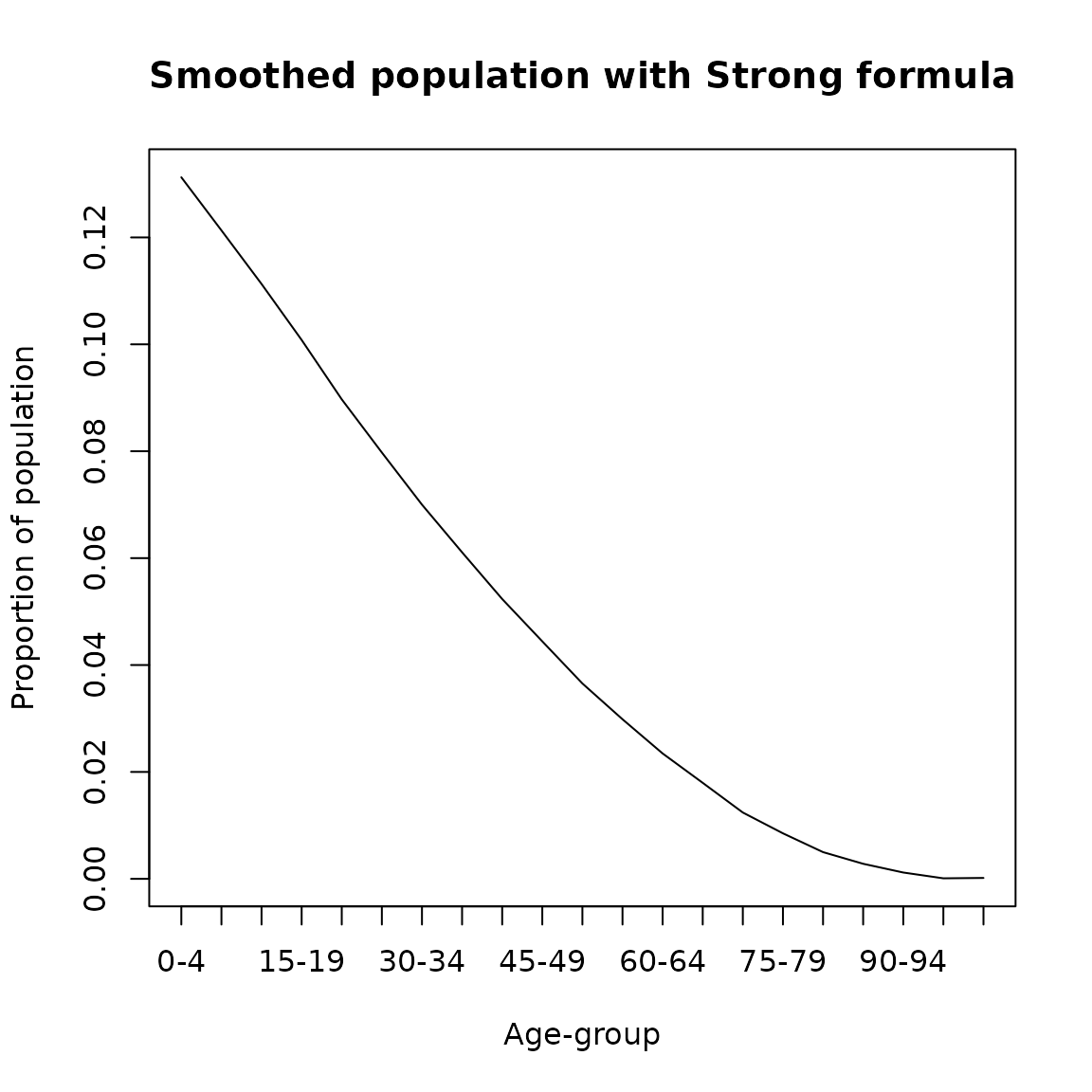

Zigzag

The implementations of this methods assumes that persons incorrectly reported in peak age groups are evenly divided between the two adjacent age groups (Feeney 2013). It relies in minimizing a measure of “roughness”: consider the difference \(R[i]\) between the number of persons in the \(i\)-th age group and the average of the numbers in adjacent age groups, \(R[i] = N[i] - (N[i -1] + N[i + 1])/2\). If the distribution displays zigzag, the \(R[i]\) will relatively large. If the distribution is smooth, they will be relatively small. This suggests taking the sum of squares of these differences as the measure of roughness (Feeney 2013). It can be implemented in DemoTools as follows


zz_result <- smooth_age_5(Value, Age, method = "Zigzag",OAG = TRUE, ageMin = 0, ageMax = 100)
plot(seq(0,100,5),zz_result/sum(zz_result,na.rm = T), type= 'l',
    ylab = 'Proportion of population',
     xlab = 'Age-group',main = 'Smoothed population with Zig Zag formula',xaxt='n')
axis(1, labels = paste0(seq(0,100,5),'-',seq(4,104,5)), at =seq(0,100,5))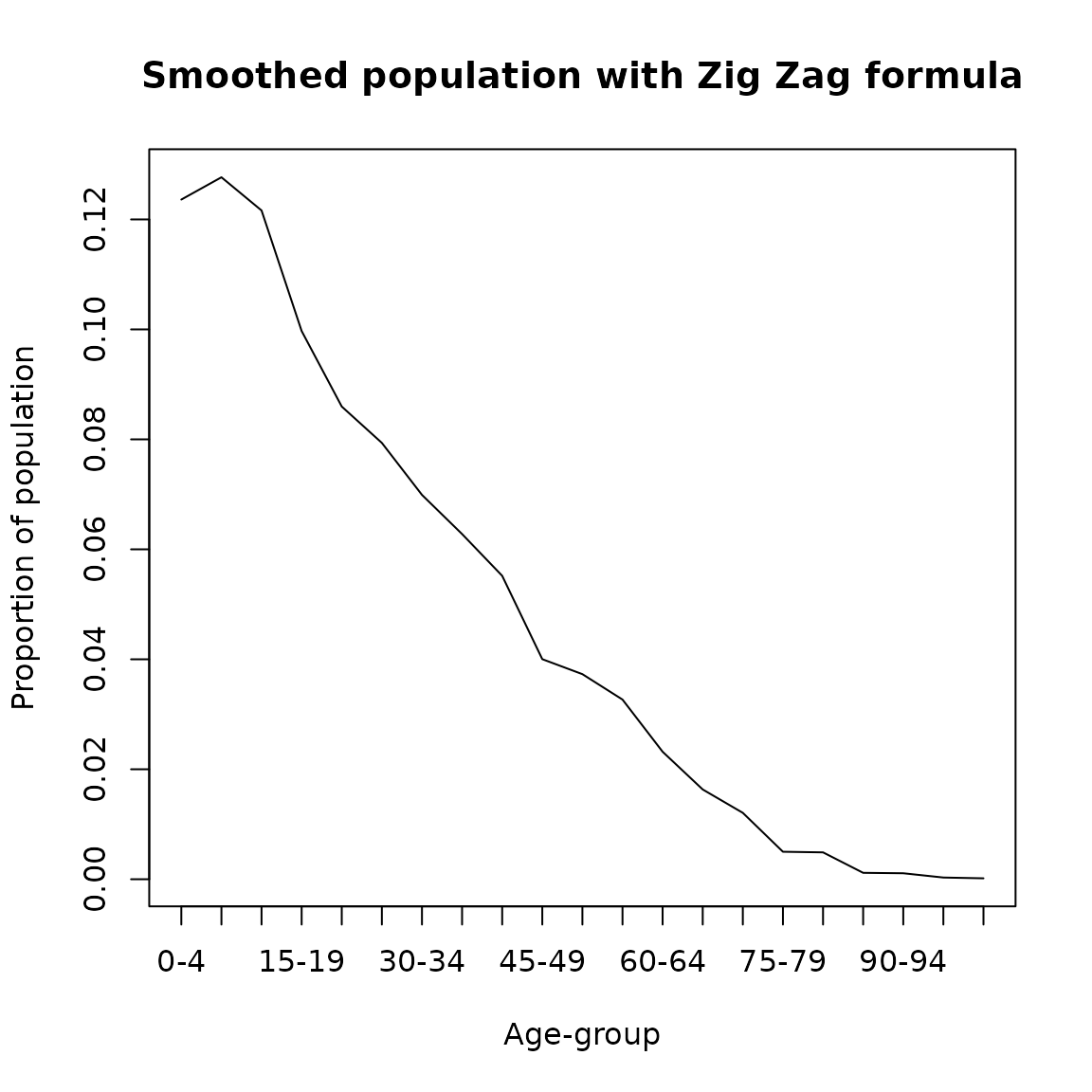

Polynomial

A more general way is to smooth through linear models. Polynomial fitting is used to smooth data over age or time fitting linear models. It can be tweaked by changing the degree and by either log or power transforming and can be used on any age groups, including irregularly spaced, single age, or 5-year age groups. It can be implemented in DemoTools with the function agesmth1 and the option poly as follows


poly_result <- agesmth1(Value, Age, method="poly", OAG = T)
plot(0:100,poly_result, type= 'l',
    ylab = 'Proportion of population',
     xlab = 'Age-group',main = 'Smoothed population with Poly formula',xaxt='n')
points(0:100,Value)
axis(1, labels =seq(0,100,5), at =seq(0,100,5))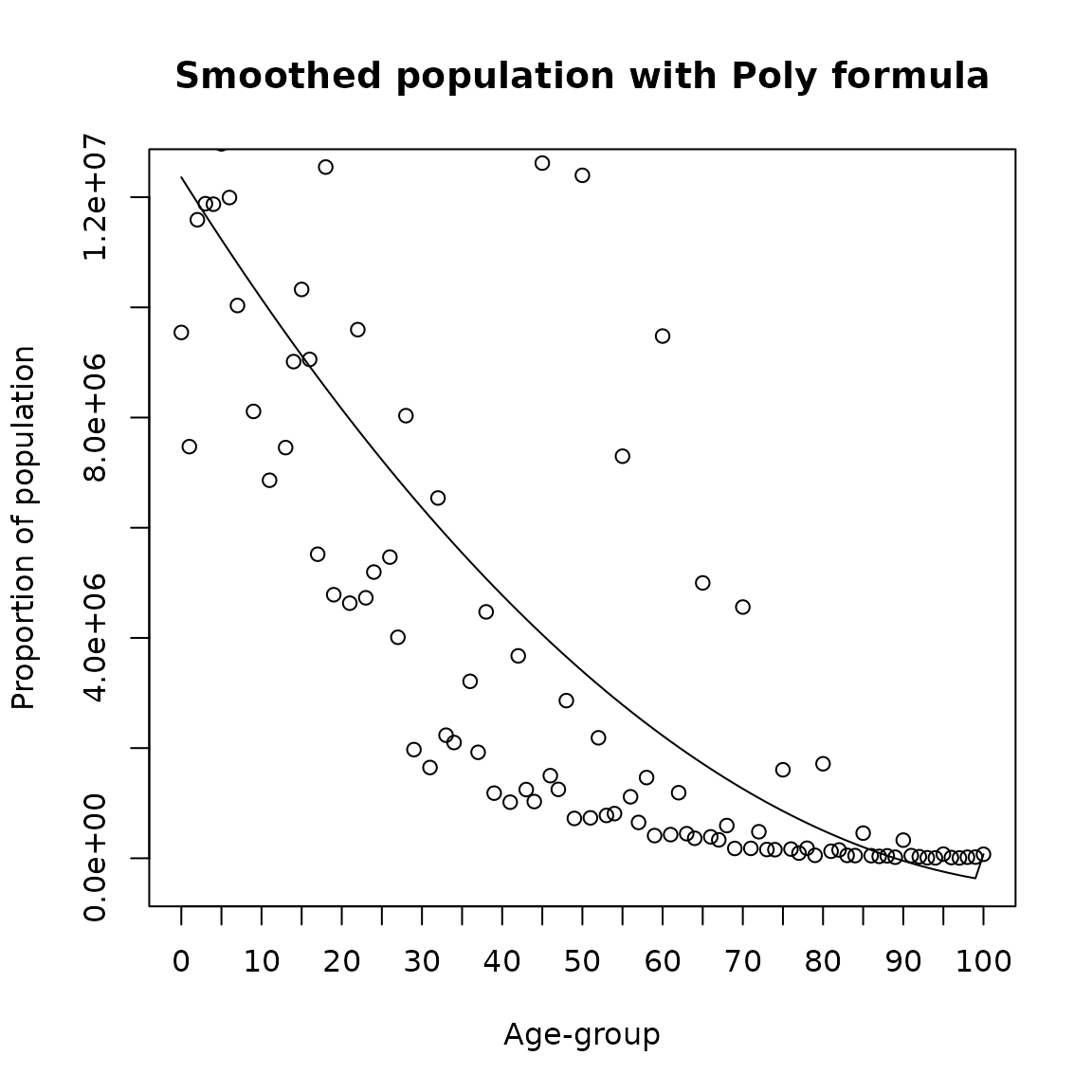

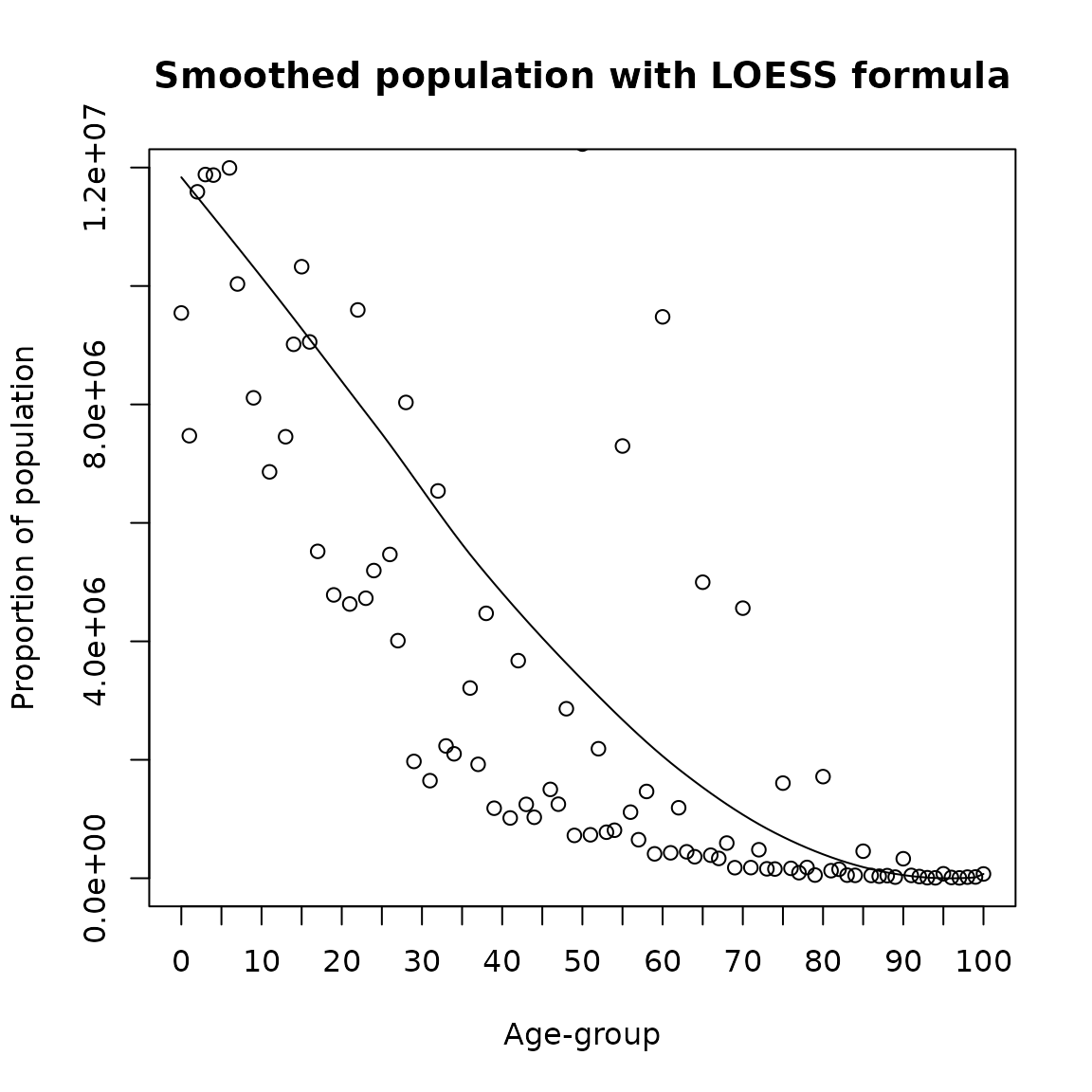
LOESS

LOESS (locally weighted smoothing) helps to smooth data over age, preserving the open age group if necessary. It is a popular tool to create a smooth line through a timeplot or scatter plot. It can be tweaked by changing the degree and by either log or power transforming and can be used on any age groups, including irregularly spaced, single age, or 5-year age groups.


loess_result <- agesmth1(Value, Age, method="loess", OAG = T)
plot(0:100,loess_result, type= 'l',
    ylab = 'Proportion of population',
     xlab = 'Age-group',main = 'Smoothed population with LOESS formula',xaxt='n')
points(0:100,Value)
axis(1, labels =seq(0,100,5), at =seq(0,100,5))

References

Arriaga, Eduardo E, Peter D Johnson, and Ellen Jamison. 1994. Population Analysis with Microcomputers. Vol. 1. Bureau of the Census.
Arriaga, Eduardo E, and others. 1968. “New Life Tables for Latin American Populations in the Nineteenth and Twentieth Centuries.” New Life Tables for Latin American Populations in the Nineteenth and Twentieth Centuries., no. 3.
Carrier, Norman H, and AM Farrag. 1959. “The Reduction of Errors in Census Populations for Statistically Underdeveloped Countries.” Population Studies 12 (3): 240–85.
Feeney, G. 2013. “Removing "Zigzag" from Age Data.” White-Papers 1 (1).
Siegel Jacob, S, and A Swanson David, eds. 2004. The Methods and Materials of Demography. 2nd ed. San Diego, USA: Elsevier Academic Press, California, USA.
Spencer, G. 1987. “Improvements in the Quality of Census Age Statistics for the Elderly” 1: 3–1.
United Nations. 1955. Manual II: Methods of Appraisal of Quality of Basic Data for Population Estimates. 23. New York: United Nations Department of International Economic; Social Affairs.